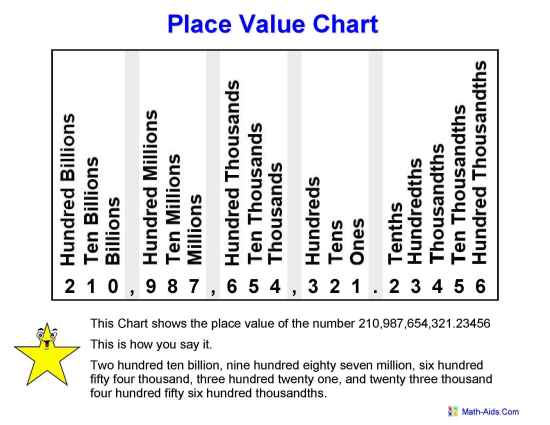
Before a person can even begin estimating and working with mental computation, they must understand how place value works. Place Value is the numerical value a digit has because of it's position in a number. Here is a great Place Value reference chart I found at Math-Aids.com:
Place value is especially important when you are trying to estimate. Typically, you are rounding to the nearest whole number for a specific place value. For example, if you were to be told to "round 364 to the nearest ten", you would have to look at the number in the ten spot; in this case 4. When rounding we decide to go up or down based on the value of a specific digit. If the digit is 4 or less we round down, if it is 5 or higher we round up. In the case of 364, the 4 tells us to round down leaving us with 360.
Mental Computation is the process of finding the exact answer to a problem mentally, without any outside supports. Supports are considered paper, pencil, calculator, etc...
There are several different techniques for solving with mental computation. Here are several examples:
Count On Technique - Method for adding when one of the addends is 1, 2, or 3. Select the larger addend first, then add by intervals until you have used the second addend. For example:
65+30= 65, 75, 85, 95
Count Back Technique - Like the Count On Technique, this method is best when used with the numbers 1, 2, or 3. Select the larger number first, then subtract by intervals until you have used the second number. For example:
430-3= 430, 429, 428, 427
Choose Compatible Numbers Technique - Look for compatible number patterns that can be solved together easily. Then continue computing like number patterns. For example, numbers that create multiples of 10 or 100. Example:
37+20+243+200= 37+20=57, 243+200=443, 443+57= 500
Break Apart Numbers Technique - Break numbers in computations up into more reasonable easy to work with numbers. For example: 264 can be broken apart to equal 100+100+60+4
Use Compensation Technique - First substitute compatible numbers to make the computation easier to deal with. Then, adjust the answer to compensate for the change you made. For example:
4.99+7.95= 5+8=13 Now compensate for the extra: 13-.06=12.94
Computational Estimation is the process of finding an answer that is relatively close to the real answer using a best guess or estimate.
Like mental computation, computational estimation has several types of techniques that can be used.
Rounding - The process of a number or numbers in a problem with the closest multiple of 10, 100, 1,000, and so on. First find the halfway point between the multiples. Anything below the half way point rounds down while anything above it rounds up. For example:
423 would round down to 420 because the 3 is below 5. 435 would round to 440 because the 5 causes you to round up.
Substitution of Compatible Numbers - Replacing some or all of the numbers in a problem with numbers that are easier to compute mentally. For example: 2,479-222 can be replaced by 2,480-220.
Front-end estimation - Use the left most digit and pretend all the other digits to the right are zeros. For example:
718-309 can be replaced with 700-300.
Front-end estimation - Use the left most digit and pretend all the other digits to the right are zeros. For example:
718-309 can be replaced with 700-300.
Clustering - In some addition problems, the numbers cluster around a common number. Find the common number and multiply by the number of addends. For example:
24, 31, 37, 28 can all be compared to 30. So, we would turn this into 30 X 4.
65+30= 65, 75, 85, 95
Count Back Technique - Like the Count On Technique, this method is best when used with the numbers 1, 2, or 3. Select the larger number first, then subtract by intervals until you have used the second number. For example:
430-3= 430, 429, 428, 427
Choose Compatible Numbers Technique - Look for compatible number patterns that can be solved together easily. Then continue computing like number patterns. For example, numbers that create multiples of 10 or 100. Example:
37+20+243+200= 37+20=57, 243+200=443, 443+57= 500
Break Apart Numbers Technique - Break numbers in computations up into more reasonable easy to work with numbers. For example: 264 can be broken apart to equal 100+100+60+4
Use Compensation Technique - First substitute compatible numbers to make the computation easier to deal with. Then, adjust the answer to compensate for the change you made. For example:
4.99+7.95= 5+8=13 Now compensate for the extra: 13-.06=12.94
Mental Multiplication Math Video (this user has many mental math videos in on his YouTube page)
Like mental computation, computational estimation has several types of techniques that can be used.
Rounding - The process of a number or numbers in a problem with the closest multiple of 10, 100, 1,000, and so on. First find the halfway point between the multiples. Anything below the half way point rounds down while anything above it rounds up. For example:
423 would round down to 420 because the 3 is below 5. 435 would round to 440 because the 5 causes you to round up.
Substitution of Compatible Numbers - Replacing some or all of the numbers in a problem with numbers that are easier to compute mentally. For example: 2,479-222 can be replaced by 2,480-220.
Front-end estimation - Use the left most digit and pretend all the other digits to the right are zeros. For example:
718-309 can be replaced with 700-300.
Front-end estimation - Use the left most digit and pretend all the other digits to the right are zeros. For example:
718-309 can be replaced with 700-300.
Clustering - In some addition problems, the numbers cluster around a common number. Find the common number and multiply by the number of addends. For example:
24, 31, 37, 28 can all be compared to 30. So, we would turn this into 30 X 4.
Examples of Front End, Clustering, and Compatible Numbers:
No comments:
Post a Comment